Tratamiento de datos y azar: U1 RA 1.3 Leyes probabilidad

En este apartado se estudiarán las leyes siguientes:

Leyes

- De multiplicación y adición.

Principio de la multiplicación

Si un evento A se puede realizar de «m» formas diferentes y luego se puede realizar otro evento B de «n» formas diferentes, el número total de formas en que pueden ocurrir A y B es igual a m x n. Es decir, ambos eventos se realizan, primero uno y luego el otro. El «y» indica multiplicación.

Ejemplo: ¿de cuántas formas se puede vestir una persona que tiene 3 pantalones y 3 camisas?

Para vestirse, la persona se pone el pantalón y luego la camisa, es decir tiene 3 x 3 = 9 opciones diferentes de vestirse.

Principio de la adición

Si un evento «A» se puede realizar de «m» maneras diferentes, y otro evento «B» se puede realizar de «n» maneras diferentes, además, si ocurre uno no puede ocurrir el otro, entonces, el evento A o el evento B, se realizarán de m+n formas. Es decir, aquí ocurre A o ocurre B. El «o» indica suma.

Ejemplo: ¿de cuántas formas se puede cruzar un río, sabiendo que se dispone de 3 botes y 4 barcos?

El río se puede cruzar en bote o en barco, es decir, tiene 3 + 4 = 7 opciones diferentes para cruzar el río. El río se cruza en bote o en barco.

Guía de ejercicios

En la siguiente guía, encontrarás muchos problemas del principio de adición y del principio de multiplicación. Resolveremos algunos en los videos:

Principio de adición y multiplicación, ejercicios propuestos PDF

En el primer video, vamos a revisar algunos conceptos importantes, así como 2 ejercicios resueltos.

https://youtu.be/BeA6saiK-_8

Nivel 2A

En el siguiente video, vienen varios ejercicios resueltos de principio aditivo y principio multiplicativo, pero aplicados a varios eventos, no solo 2.

https://youtu.be/LCHDHOxAlSo

Nivel 2B

Ahora vienen algunos ejercicios de conteo de números, usando el principio de multiplicación.

https://youtu.be/RU4oHCRU-LY

Nivel 2C

Veamos ahora un ejercicio del principio de multiplicación de un examen.

https://youtu.be/Wj1FUNhf574

Nivel 3

Vienen ahora dos problemas complicados, uno de rutas y otro de conteo de números.

https://youtu.be/0sfjBiKr7Jc

- Condicional

Si tenemos dos eventos, A y B, la probabilidad condicional de que ocurra el evento A, dado que ha ocurrido el evento B, se representa como P(A|B), y se calcula de la siguiente manera:

Fórmula:

En un diagrama de Venn, veríamos los eventos A y B de la siguiente manera:

La condición, es que se ha realizado en el evento B, por lo tanto, nuestro diagrama de Venn quedaría reducido a:

or ello, podemos ver que el universo está representado por la probabilidad de B, y dentro de ese universo, la probabilidad de que ocurra A, está representada por la probabilidad de A ∩ B.

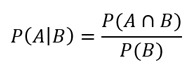
En algunos problemas, puede que sea necesario calcular la probabilidad de que ocurra el evento B, dado que ha ocurrido A. En ese caso, simplemente invertimos el orden de las variables:

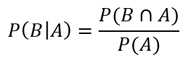
probabilidad condicional ejercicios resueltos

Ejemplo 1:

Si P(A) = 0,6 ; P(B) = 0,4 y P(A∩B)=0,18. Calcular:

a) P(A|B)
b) P(B|A)

Solución:
En este problema, simplemente vamos a reemplazar los datos en la fórmula.

a) Usamos la fórmula de probabilidad condicional:

b) Usamos la fórmula de fórmula de probabilidad condicional, teniendo en cuenta que vamos a calcular la probabilidad de que ocurra B, dado que ha ocurrido A.

Ejemplo 2:

Al 25% de tus amigos le gusta la fresa y el chocolate, mientras que al 60% le gusta el chocolate. ¿Cuál es la probabilidad de que a un amigo que le gusta el chocolate, le guste la fresa?

Solución:
Vamos a trabajar con 2 eventos: que a un amigo le guste la fresa, y que a un amigo le guste el chocolate.

Evento A: que a un amigo le gusten los fresa. P(A) = ?
Evento B: que a un amigo le guste el chocolate. P(B) = 60 %.
Evento A y B: que a un amigo le guste la fresa y el chocolate. P(A∩B) = 25 %.

Ahora calculamos la probabilidad de que a un amigo le guste la fresa, dado que le gusta el chocolate.

La probabilidad de que a un amigo le guste la fresa dado que le gusta el chocolate es del 41,67 %.

Ejemplo 3:

El 76 % de los estudiantes de Ingeniería Civil han aprobado resistencia de materiales y el 45 % aprobaron estática. Además, el 30 % aprobaron resistencia de materiales y estática. Si Camilo aprobó resistencia de materiales, ¿qué probabilidad tiene de haber aprobado también estática?

Solución:
Vamos a trabajar con 2 eventos: aprobar resistencia de materiales, y aprobar estática.

Evento A: aprobar resistencia de materiales. P(A) = 76 %.
Evento B: aprobar estática. P(B) = 45 %.
Evento A y B: aprobar resistencia de materiales y estática. P(A∩B) = 30 %, y es lo mismo que: P(B∩A) = 30 %

Ahora calculamos la probabilidad de aprobar estática, dado que se aprobó resistencia de materiales.

Para Camilo, la probabilidad de aprobar estática, dado que aprobó resistencia de materiales es de 39,47 %.

Guía de ejercicios

En la siguiente guía encontrarás muchísimos problemas de probabilidades, algunos los de probabilidad condicional en el video.

Probabilidades, ejercicios propuestos PDF

Video

Viene ahora el video que hemos preparado con muchos problemas de probabilidad condicional.

https://youtu.be/dStF9z7tjZU

- Bayes

El teorema de Bayes expresa la probabilidad de que ocurra el evento A, dado que ha ocurrido B, en función de la probabilidad de que ocurra B dado que ha ocurrido A, de la probabilidad de A y de la probabilidad de B. La fórmula del teorema de Bayes es la siguiente:

Como se puede apreciar, el teorema de Bayes permite calcular la probabilidad de que ocurra un evento, a partir de valores conocidos de otras probabilidades relacionadas al evento.

El teorema o regla de Bayes fue planteado por el matemático y religioso inglés Thomas Bayes. Este teorema fue publicado en el año 1763, dos años después de la muerte de Bayes.

Este teorema lo encontramos de dos formas diferentes, en su forma simple y en su forma extendida, las cuales revisaremos a continuación, además de muchos ejemplos y ejercicios.

Forma simple del teorema de Bayes:

La forma simple de este teorema es la que mencionamos al inicio del artículo y es la siguiente:

Donde:

A y B son eventos, y además: P(B) ≠ 0.
P(A|B): es la probabilidad de que ocurra A, dado que ha ocurrido B.
P(B|A): es la probabilidad de que ocurra B, dado que ha ocurrido A.
P(A): es la probabilidad de que ocurra A.
P(B): es la probabilidad de que ocurra B.

En la práctica tiene muchísimas aplicaciones, por ejemplo, conociendo la probabilidad de que una persona tenga fiebre dado que tiene gripe, nos permite calcular la probabilidad de que una persona que tiene gripe, dado que tiene fiebre. Tiene, además, aplicaciones importantísimas en la detección del cáncer y otras enfermedades.

Ejemplo 1:

En la academia de Matemóvil, la probabilidad de que a un alumno seleccionado al azar le guste el helado es del 60 %, mientras que la probabilidad de que a un alumno le guste la torta es del 36 %. Además, se sabe que la probabilidad de que a un alumno le guste la torta dado que le gusta el helado es del 40 %. Calcular la probabilidad de que a un alumno le guste el helado, dado que le gusta la torta.

Solución:

Primero definimos los 2 eventos con los que vamos a trabajar:

h: que a un alumno le guste el helado.
t: que a un alumno le guste la torta.

Tenemos los siguientes datos:

P(h) = 0,6.
P(t) = 0,36.
P(t|h) = 0,4.

Nos piden calcular P(h|t).

Aplicamos el teorema de Bayes:

Entonces, la probabilidad de que un alumno le guste el helado dado que le gusta la torta es de 0,6667 o 66,67 %.

Forma extendida del teorema de Bayes:

Esta forma extendida es la que encontrarás en la mayoría de libros de estadística. Emplea las particiones del espacio muestral.

Guía de ejercicios

En la guía de ejercicios de probabilidades, encontrarás algunos ejercicios del teorema de Bayes que resolveremos juntos en los videos que vienen líneas abajo.

Ejercicios de probabilidades

Video

A continuación, viene el video que hemos preparado del teorema de Bayes.

https://youtu.be/CP4ToX5Tyvw

/*En equipos de 5 integrantes deberán investigar las leyes:

Deberán exponer las leyes en una presentación de Power Point y poner un ejercicio por cada Ley.

Cada equipo deberá entregar al grupo un problema distinto a los demás equipos para que lo resuelvan los alumnos en equipos de 5 integrantes.

La exposición deberá contener la ley y dos ejemplos explicados por los alumnos.

Cada equipo evaluará el problema que dejará para el grupo.

Como resultado de la exposición de cada equipo, deberán entregar la lista de los alumnos y la calificación de la evaluación del problema que dejaron por equipos. */

Nombre del archivo:
Grupo-Primer apellido Segundo Apellido_Nombre de la ley.pdf